Description Link to heading
99. Recover Binary Search Tree (Medium)
You are given the root of a binary search tree (BST), where the values of exactly two nodes of
the tree were swapped by mistake. Recover the tree without changing its structure.
Example 1:
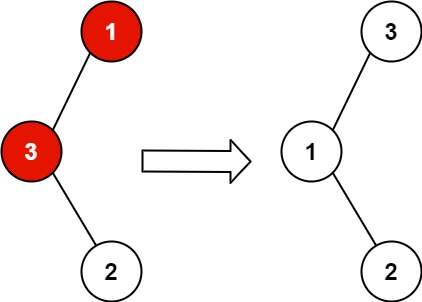
Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
Example 2:
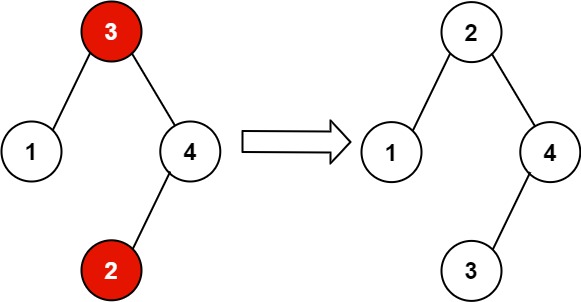
Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST
valid.
Constraints:
- The number of nodes in the tree is in the range
[2, 1000]. -2³¹ <= Node.val <= 2³¹ - 1
Follow up: A solution using O(n) space is pretty straight-forward. Could you devise a constant
O(1) space solution?
Solution Link to heading
In this context, we shall consider a solution with a time complexity of $O(1)$. Initially, it is worth noting that when conducting an in-order traversal of a binary search tree, the node values strictly follow an ascending order. Consequently, we may exploit this insight to identify the two nodes that have been swapped.
Let us contemplate an ascending sequence and the exchange of any two elements within it. If these two elements happen to be adjacent, then during our traversal, a situation will arise wherein $a_{i} < a_{i - 1}$. On the other hand, if these two elements are not adjacent, we will encounter $a_{i} < a_{i - 1}$ twice. We shall store all such pairs of elements where $a_{i} < a_{i - 1}$ in an array called vec. Therefore, it follows that vec.size() == 2 || vec.size() == 4, and to rectify the situation, we need only swap the values of the first and last elements in the array.
As we traverse in an in-order manner, we can employ the prev variable to represent the pointer to the previous node in the traversal. By comparing the values of root->val and prev->val, we can ascertain whether the sequence adheres strictly to the increasing order. If it does not, we shall consecutively push_back both root and prev into the vec array, and finally, perform a swap between vec[0]->val and vec.back()->val.
Below is a template for an in-order traversal incorporating the prev variable:
void midtra(TreeNode *root, TreeNode **prev) {
if (root == nullptr) {
return;
}
midtra(root->left, prev);
*prev = root;
midtra(root->right, prev);
}
Code Link to heading
class Solution {
public:
void midtra(TreeNode *root, TreeNode **prev, vector<TreeNode *> &wrong) {
if (root == nullptr) {
return;
}
midtra(root->left, prev, wrong);
if (*prev != nullptr) {
if (root->val < (*prev)->val) {
wrong.push_back(*prev);
wrong.push_back(root);
}
}
*prev = root;
midtra(root->right, prev, wrong);
}
void recoverTree(TreeNode *root) {
// 中序遍历
vector<TreeNode *> wrong;
TreeNode *node = nullptr;
midtra(root, &node, wrong);
swap(wrong[0]->val, wrong.back()->val);
}
};