Description Link to heading
153. Find Minimum in Rotated Sorted Array (Medium)
Suppose an array of length n sorted in ascending order is rotated between 1 and n times.
For example, the array nums = [0,1,2,4,5,6,7] might become:
[4,5,6,7,0,1,2]if it was rotated4times.[0,1,2,4,5,6,7]if it was rotated7times.
Notice that rotating an array [a[0], a[1], a[2], ..., a[n-1]] 1 time results in the array
[a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Given the sorted rotated array nums of unique elements, return the minimum element of this
array.
You must write an algorithm that runs in O(log n) time.
Example 1:
Input: nums = [3,4,5,1,2]
Output: 1
Explanation: The original array was [1,2,3,4,5] rotated 3 times.
Example 2:
Input: nums = [4,5,6,7,0,1,2]
Output: 0
Explanation: The original array was [0,1,2,4,5,6,7] and it was rotated 4 times.
Example 3:
Input: nums = [11,13,15,17]
Output: 11
Explanation: The original array was [11,13,15,17] and it was rotated 4 times.
Constraints:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000- All the integers of
numsare unique. numsis sorted and rotated between1andntimes.
Solution Link to heading
The array after rotating is like the follow picture:
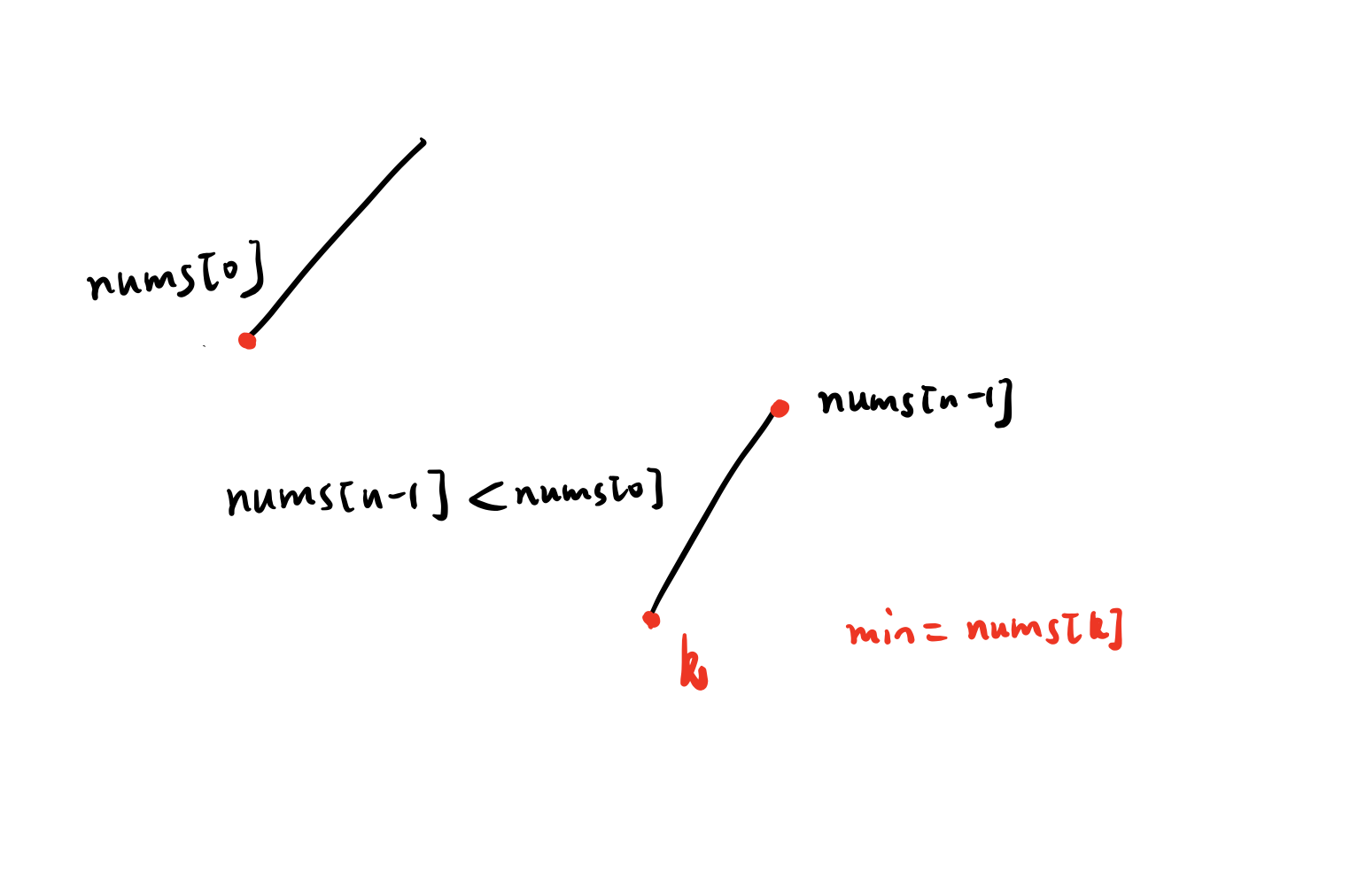
We can use binary search ,int left = 0, right = nums.size(), n = nums.size(), if nusm[mid] <= nums[n - 1], mid >= k; otherwise, mid < k.
It also works for special cases.
Code Link to heading
class Solution {
public:
int findMin(vector<int> &nums) {
int n = nums.size();
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] <= nums[n - 1]) { // it means `mid >= k`
right = mid;
} else { // it means `mid < k`
left = mid + 1;
}
}
return nums[left % n];
}
};